Lake Acidity Study

This data set was derived by Douglas and Delampady (1990) from the Eastern Lakes Survey of 1984. It contains measurements of 1789 lakes in three Eastern US regions: Northeast, Upper Midwest and Southeast. Of interest is the dependence of the water pH level ($ph$) on the calcium concentration in $\log_{10}$ milligrams per liter ($t_1$) and the geographical location ($t_2=(x_1,x_2)$ where $x_1$=latitude and $x_2$=longitude). Gu and Wahba (1993a) analyzed this data set using SS ANOVA models. As in Gu and Wahba (1993a), we use a subset of 112 lakes in the southern Blue Ridge mountains area.

We use this data set to illustrate how to fit a cubic spline, a cubic spline with correlated random errors, a SLM and an SS ANOVA model.

First, we fit a cubic spline to $ph$ using one variable calcium ($t_1$)

$$\begin{eqnarray*} \mbox{{\tt pH}}(t_1) = f(t_1) + \epsilon(t_1) \end{eqnarray*}$$

where $f\in W_2([0,1])$.

> acid.fit1 <- ssr(ph~t1, rk=cubic(t1), data=acid, scale=T)
> summary(acid.fit1)
...
GCV estimate(s) of smoothing parameter(s) : 3.84e-06
Equivalent Degrees of Freedom (DF):  8.21
Estimate of sigma:  0.281
> anova(acid.fit1)

Testing H_0: f in the NULL space

     test.value simu.size simu.p-value 
LMP 0.003634651       100         0.04
GCV 0.008239078       100         0.02

Both p-values from the LMP and GCV tests are small, indicating that a simple linear model is not sufficient to describe the relationship. This can be confirmed by looking at the fitted function and its projections onto ${\cal H}_0$ and ${\cal H}_1$. A linear model is equivalent to the projection onto ${\cal H}_1$ being zero. The following statements compute posterior means and standard deviations for the projections onto ${\cal H}_0$ with terms=c(1,1,0), the projections onto ${\cal H}_1$ with terms=c(0,0,1), and the overall fit with terms=c(1,1,1).

 
> grid <- data.frame(t1=seq(min(acid$t1), max(acid$t1), len=100))
> tm <- matrix(c(1,1,0,0,0,1,1,1,1), ncol=3, byrow=T) 
> p.acid.fit1 <- predict(acid.fit1, grid, terms=tm)

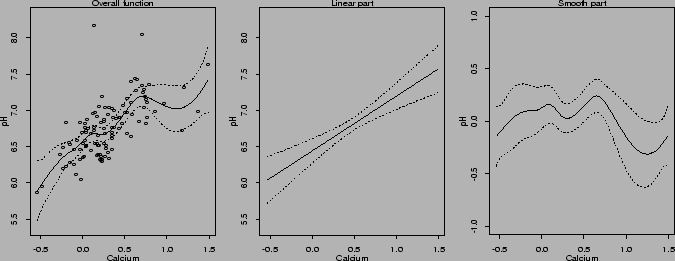
Figure shows the fitted function and its projections. The nonlinear part is small, but different from zero.

Figure: Left: circles are observations, solid line is the cubic spline fit. Middle: solid line is the projection of the overall function to the null space ${\cal H}_0$. Right: solid line is the projection of the overall function to the space ${\cal H}_1$. Dotted lines are 95% Bayesian confidence intervals.

pH observations close in geographic locations are often correlated. Suppose that we want to use spherical spatial correlation structure with nugget effect for the variable location $t_2=(x_1,x_2)$. That is, regard random errors $\epsilon$ as a function of $t_2$, and assume

$$\begin{eqnarray*} \mbox{Cov} (\epsilon(s_2),\epsilon(t_2)) = \left\{ \begin{arr... ..._2,t_2) \le r,\\ \sigma^2, & d(s_2,t_2)=0, \end{array} \right. \end{eqnarray*}$$

where $c$ is the nugget effect, $d(s_2,t_2)$ is the Euclidean distance between $s_2$ and $t_2$, and $r$ is the range parameter.

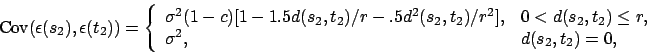
> acid$s1 <- (acid$t1-min(acid$t1))/diff(range(acid$t1))
> acid.fit2 <- ssr(ph~s1, rk=cubic(s1), data=acid,
                   corr=corSpher(form=~x1+x2,nugget=T), spar="m")
> acid.fit2
...
Coefficients (d):
(Intercept)          s1 
   6.221757    1.264431 

GML estimate(s) of smoothing parameter(s) : 4.645508 
Equivalent Degrees of Freedom (DF):  2.000284 
Estimate of sigma:  0.2994075 
Correlation structure of class corSpher representing
     range     nugget 
0.03646616 0.68530949

We plot in Figure fitted curves from acid.fit1, acid.fit2 and acid.fit5. Notice the effect of the correlation on the smoothing parameter and the fit. Equivalent degrees of freedom for $f$ decreased from 8.21 to 2.00. The new fit is linear. The smaller smoothing parameter in the first fit might be caused by the spatial correlation.

Figure: Points are observations. Lines are fitted curves from three models.

We can also model the effect of location directly as a covariate. We consider two approaches to model location effect: use random effects with exponential spatial correlation structure (similar to Kriging), and use thin plate splines.

For the first approach, we consider

$$\mbox{{\tt pH}}(t_1,t_2) = f(t_1) + \beta_1 x_1 + \beta_2 x_2 + u(t_2) + \epsilon(t_1,t_2) ,$$ (76)

where $f\in W_2([0,1])$, $u(t_2)$ is a spatial process and $\epsilon(t_1,t_2)$ are random errors independent of the spatial process. Model () separates the contribution of the spatial correlation to random errors in acid.fit2 from other sources, and regard the spatial process as part of the signal. To show different options, we now assume an exponential correlation structure. Specifically, we assume $u(t_2)$ in () is a mean zero process with

$$\mbox{Cov} (u(s_2),u(t_2))=\left\{ \begin{array}{ll} \sigma^... ...&d(s_2,t_2)>0\\ \sigma^2, & d(s_2,t_2)=0, \end{array} \right.$$

where $c$, $d(s_2,t_2)$ and $r$ are the same as those defined in the spherical correlation structure. Note that we include the linear effects of location in the fixed effects. This will allow us to compare with the fit of a thin plate spline model later.

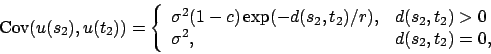
Denote $\mbox{\boldmath$t$}$ as the vector of design points for $t_2$. Let $u(\mbox{\boldmath$t$})$ be the vector of the $u$ process evaluated at design points. $u(\mbox{\boldmath$t$})$ are random effects and $u(\mbox{\boldmath$t$}) \sim \mbox{N} (0, \sigma^2D)$, where $D$ depends parameters $c$ and $r$. Again, the SLM model () cannot be fitted directly using slm since $D$ depends on the range parameter $r$ nonlinearly. We fit model () in two steps. We first regard $u(\mbox{\boldmath$t$})$ as part of random error, estimate the range parameter, and calculate the estimated covariance matrix without nugget effect:

> temp <- ssr(ph~t1+x1+x2, rk=tp(t1), data=acid,
              corr=corExp(form=~x1+x2, nugget=T), spar="m")	
> tau <- coef(temp$cor.est, F)
> D <- corMatrix(initialize(corExp(tau[1],form=~x1+x2), data=acid))

Consider the estimated $D$ as the true covariance matrix. Then we can calculate the Cholesky decomposition of $D$ as $D = ZZ^T$, and transform the random effects $u(\mbox{\boldmath$t$})=Z \mbox{\boldmath$b$}$, where $\mbox{\boldmath$b$}\sim \mbox{N}(0,\sigma_1^2 I)$. Now we are ready to fit the transformed SLM:

> Z <- chol.new(D)
> acid.fit3 <- slm(ph~t1+x1+x2, rk=tp(t1), data=acid,
                   random=list(pdIdent(~Z-1)))
> summary(acid.fit3)
...
Coefficients (d):
(Intercept)          t1          x1          x2 
  6.5483884   0.6795706  -8.3694493   2.1135023 

GML estimate(s) of smoothing parameter(s) : 0.0005272899 
Equivalent Degrees of Freedom (DF):  4.000179 
Estimate of sigma:  0.002725062

We then calculate the estimated effect of calcium:

grid1 <- data.frame(t1=seq(min(acid$t1), max(acid$t1), len=100),
                    x1=min(acid$x1), x2=min(acid$x2))
p.acid.fit3.t1 <- intervals(acid.fit3, grid1, terms=c(0,1,0,0,1))

Suppose that we want to calculate the location effect on grid points $\mbox{\boldmath$s$}$. Let $u(\mbox{\boldmath$s$})$ be the vector of the $u$ process evaluated at elements in $\mbox{\boldmath$s$}$. Let $R=\mbox{Cov} (u(\mbox{\boldmath$s$}),u(\mbox{\boldmath$t$}))$. Then $\hat{u}(\mbox{\boldmath$s$})=R D^{-1} \hat{u}(\mbox{\boldmath$t$}) = R Z^{-T} \hat{\mbox{\boldmath$b$}}$.

grid2 <- expand.grid(
                x1=seq(min(acid$x1)-.001,max(acid$x1)+.001, len=20),
                x2=seq(min(acid$x2)-.001,max(acid$x2)+.001, len=20))
newdata <- data.frame(y1=c(acid$x1,grid2$x1), y2=c(acid$x2,grid2$x2))
RD <- corMatrix(initialize(corExp(tau[1], form=~y1+y2), data=newdata))
R <- RD[(length(acid$x1)+1):length(newdata$y1),1:length(acid$x1)] 
u.new <- R%*%t(solve(Z))%*%as.vector(acid.fit3$lme.obj$coef$random[[2]])
p.acid.fit3.t2 <- acid.fit3$lme.obj$coef$fixed[3]*grid2$x1+
                  acid.fit3$lme.obj$coef$fixed[4]*grid2$x2+u.new

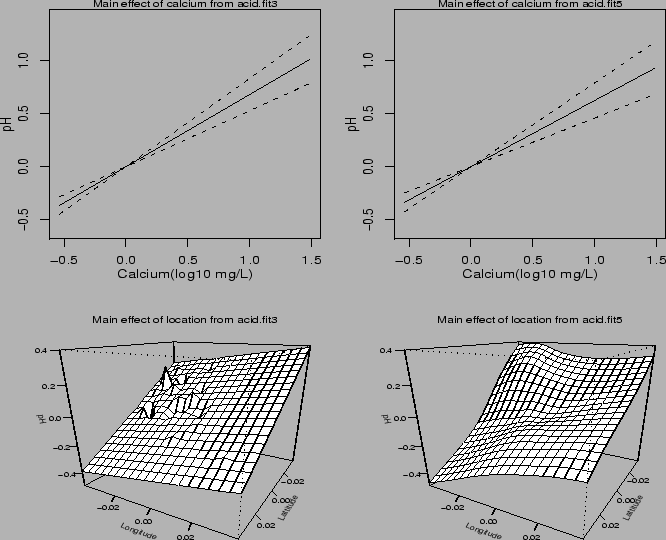
Figure plots the estimated main effects of $t_1$ and $t_2=(x_1,x_2)$ on the left panel.

As the second approach, we consider the same thin plate spline model as in Gu and Wahba (1993a). Specifically, we use a TPS with $d=1$ and $m=2$ to model the effect of calcium, and a TPS with $d=2$ and $m=2$ to model the effect of location. Then we have the following SS ANOVA model

$$f(t_1, t_2)= \mu + \alpha t_1 + \beta x_1 + \gamma x_2 + s_1... ... sl_{12}^1(t_1,x_1) + sl_{12}^2(t_1,x_2) + ss_{12}(t_1,t_2).$$

Components on the right hand side are constant, linear main effect of $t_1$, linear main effect of $x_1$, linear main effect of $x_2$, smooth main effect of $t_1$, smooth main effect of $t_2$, linear-smooth interaction between $t_1$ and $t_2$, smooth-linear interaction between $t_1$ and $x_1$, smooth-linear interaction between $t_1$ and $x_2$, and smooth-smooth interaction between $t_1$ and $t_2$.

> acid.fit4 <- ssr(ph~t1+x1+x2, rk=list(tp(t1), tp(list(x1,x2)), 
                rk.prod(kron(t1),tp(list(x1,x2))), rk.prod(kron(x1),tp(t1)), 
                rk.prod(kron(x2),tp(t1)), rk.prod(tp(t1),tp(list(x1,x2)))),
                data=acid, spar="m")
> summary(acid.fit4)
...
Coefficients (d):
 (Intercept)        t1        x1       x2 
    6.555506 0.6235892 -8.783944 1.974596

GML estimate(s) of smoothing parameter(s) : 1.816737e+04 
3.600865e-03 2.710276e+01 2.759507e+00 1.992876e+01 1.440841e-01 
Equivalent Degrees of Freedom (DF):  10.7211 
Estimate of sigma:  0.2560693

Since the smoothing parameters corresponding to the interaction terms are large, it is easy to check that these interaction terms are small. Thus we reduce to the following additive model with main effects only

$$\begin{eqnarray*} f(t_1, t_2)= \mu + \alpha t_1 + \beta x_1 + \gamma x_2 + s_1(t_1) + s_2(t_2). \end{eqnarray*}$$

> acid.fit5 <- update(acid.fit3,  rk=list(tp(t1), tp(list(x1,x2))))
> summary(acid.fit5)
... ...
Coefficients (d):
 (Intercept)        t1        x1       x2 
    6.555502 0.6235885 -8.783569 1.974339

GML estimate(s) of smoothing parameter(s) : 6.045750e+03 3.600423e-03 
Equivalent Degrees of Freedom (DF):  10.72108 
Estimate of sigma:  0.2560684
> grid3 <- data.frame(t1=seq(min(acid$t1), max(acid$t1), len=100),
                      x1=min(acid$x1), x2=min(acid$x2))
> p.acid.fit5.t1 <- predict(acid.fit5, grid3, terms=c(0,1,0,0,1,0))
> grid4 <- expand.grid(t1=min(acid$t1),
                       x1=seq(min(acid$x1), max(acid$x1), len=20),
                       x2=seq(min(acid$x2), max(acid$x2), len=20))
> p.acid.fit5.t2 <- predict(acid.fit5, grid4, terms=c(0,0,1,1,0,1))

Figure plots the estimated main effects of $t_1$ and $t_2=(x_1,x_2)$ on the right panel. It is seen that the estimates of the calcium main effects are almost identical. The estimates of the location main effects have a similar pattern. The estimate from acid.fit5 is smoother.

> grid3 <- data.frame(t1=seq(min(acid$t1), max(acid$t1), len=100),
                      x1=min(acid$x1), x2=min(acid$x2))
> p.acid.fit5.t1 <- predict(acid.fit5, grid3, terms=c(0,1,0,0,1,0))
> grid4 <- expand.grid(t1=min(acid$t1),
                       x1=seq(min(acid$x1), max(acid$x1), len=20),
                       x2=seq(min(acid$x2), max(acid$x2), len=20))
> p.acid.fit5.t2 <- predict(acid.fit5, grid4, terms=c(0,0,1,1,0,1))

Figure: Plots of estimated main effects. Left: estimates from acid.fit3. Right: estimates from acid.fit5. First row: solid lines are the estimated main effects of calcium, and dotted lines are 95% confidence intervals. Second row: estimated main effects of location.