This dataset comes from a study of cold tolerance of a ![]() grass
species, Echinochloa crus-galli, described in Potvin et al. (1990)
and Pinheiro and Bates (2000). A total of twelve four-week-old
plants were used in the study. There were two types of
plants: six from Quebec and six from Mississippi. Two treatments,
nonchilling and chilling, were assigned to three plants of each type.
Nonchilled plants were kept at
grass
species, Echinochloa crus-galli, described in Potvin et al. (1990)
and Pinheiro and Bates (2000). A total of twelve four-week-old
plants were used in the study. There were two types of
plants: six from Quebec and six from Mississippi. Two treatments,
nonchilling and chilling, were assigned to three plants of each type.
Nonchilled plants were kept at ![]() C and chilled plants were
subject to 14 hours of chilling at
C and chilled plants were
subject to 14 hours of chilling at ![]() C. After 10 hours of recovery
at
C. After 10 hours of recovery
at ![]() C, CO
C, CO![]() uptake rates (in
uptake rates (in ![]() ) were measured
for each plant at seven concentrations of ambient CO
) were measured
for each plant at seven concentrations of ambient CO![]() in increasing,
consecutive order. Plots of observations are shown in Figure
in increasing,
consecutive order. Plots of observations are shown in Figure ![]() as circles. The objective of the experiment was to evaluate the effect
of plant type and chilling treatment on the CO
as circles. The objective of the experiment was to evaluate the effect
of plant type and chilling treatment on the CO![]() uptake.
uptake.
Pinheiro and Bates (2000) gave detailed analyses of
this dataset based on NLMMs using their software nlme.
They reached the following model:
> options(contrasts=rep("contr.treatment", 2))
> co2.fit1 <- nlme(uptake~exp(a1)*(1-exp(-exp(a2)*(conc-a3))),
fixed=list(a1+a2~Type*Treatment,a3~1),
random=a1~1, groups=~Plant, data=CO2,
start=c(log(30),0,0,0,log(0.01),0,0,0,50))
> co2.fit1
Nonlinear mixed-effects model fit by maximum likelihood
Model: uptake ~ exp(a1) * (1 - exp(-exp(a2) * (conc - a3)))
Data: CO2
AIC BIC logLik
393.2869 420.0259 -185.6434
Random effects:
Formula: a1 ~ 1 | Plant
a1.(Intercept) Residual
StdDev: 0.08221494 1.857658
Fixed effects: list(a1 + a2 ~ Type * Treatment, a3 ~ 1)
Value Std.Error DF t-value p-value
a1.(Intercept) 3.73338 0.052536 64 71.06301 <.0001
a1.TypeMississippi -0.29080 0.075535 64 -3.84990 0.0003
a1.Treatmentchilled -0.07274 0.074633 64 -0.97459 0.3334
a1.TypeMississippi:Treatmentchilled -0.51321 0.109733 64 -4.67688 <.0001
a2.(Intercept) -4.57570 0.086116 64 -53.13387 <.0001
a2.TypeMississippi -0.09635 0.103950 64 -0.92687 0.3575
a2.Treatmentchilled -0.17048 0.091377 64 -1.86565 0.0667
a2.TypeMississippi:Treatmentchilled 0.70555 0.205851 64 3.42748 0.0011
a3 49.98833 4.576255 64 10.92341 <.0001
...
Fits of model (![]() ) are plotted in Figure
) are plotted in Figure ![]() as dotted lines.
Based on model (
as dotted lines.
Based on model (![]() ), one may conclude that the CO2 uptake is
higher for plants from Quebec and that chilling, in general,
results in lower uptake, and its effect on Mississippi plants
is much larger than on Quebec plants. These conclusions
are comparable to the results in Potvin et al. (1990).
), one may conclude that the CO2 uptake is
higher for plants from Quebec and that chilling, in general,
results in lower uptake, and its effect on Mississippi plants
is much larger than on Quebec plants. These conclusions
are comparable to the results in Potvin et al. (1990).
We aim to use this dataset to demonstrate how to fit SNM models with
covariates, and how to check if an NLMM is appropriate. As an extension of
(![]() ), we fit the following SNM model
), we fit the following SNM model
Note that ![]() in (
in (![]() ) is excluded from (
) is excluded from (![]() )
to make
)
to make ![]() free of constraint on the vertical scale. We need the side conditions that
free of constraint on the vertical scale. We need the side conditions that
![]() and
and ![]() for
for ![]() to separate
to separate ![]() from
from ![]() .
The first condition reduces
.
The first condition reduces ![]() to
to
![]() and is
satisfied by all functions in
and is
satisfied by all functions in ![]() . We do not enforce the second condition
because it is satisfied by all reasonable estimates. Thus the null space for
. We do not enforce the second condition
because it is satisfied by all reasonable estimates. Thus the null space for
![]() becomes
becomes
![]() and the model space is
and the model space is
![]() . The penalty is still
. The penalty is still
![]() .
.
With the initial values chosen from the NLMM fit, our program converged after 5 iterations.
> M <- model.matrix(~Type*Treatment, data=CO2)[,-1]
> co2.fit2 <- snm(uptake~exp(a1)*f(exp(a2)*(conc-a3)),
func=f(u)~list(~I(1-exp(-u))-1,lspline(u, type="exp")),
fixed=list(a1~M-1,a3~1,a2~Type*Treatment),
random=list(a1~1), group=~Plant, verbose=T,
start=co2.fit1$coe$fixed[c(2:4,9,5:8)], data=CO2)
> summary(co2.fit2)
Semi-parametric Nonlinear Mixed Effects Model fit
Model: uptake ~ exp(a1) * f(exp(a2) * (conc - a3))
Data: CO2
AIC BIC logLik
406.4864 441.625 -188.3760
Random effects:
Formula: a1 ~ 1 | Plant
a1.(Intercept) Residual
StdDev: 0.09304172 1.816200
Fixed effects: list(a1 ~ M - 1, a3 ~ 1, a2 ~ Type * Treatment)
Value Std.Error DF t-value p-value
a1.MTypeMississippi -0.28569 0.055952 65 -5.10591 <.0001
a1.MTreatmentchilled -0.07212 0.054741 65 -1.31739 0.1923
a1.MTypeMississippi:Treatmentchilled -0.54879 0.099184 65 -5.53309 <.0001
a3 50.67565 4.226094 65 11.99113 <.0001
a2.(Intercept) -4.56698 0.085130 65 -53.64708 <.0001
a2.TypeMississippi -0.12162 0.098575 65 -1.23377 0.2217
a2.Treatmentchilled -0.16161 0.087009 65 -1.85740 0.0678
a2.TypeMississippi:Treatmentchilled 0.81924 0.211587 65 3.87187 0.0003
...
GCV estimate(s) of smoothing parameter(s): 1.864811
Equivalent Degrees of Freedom (DF): 4.867178
Converged after 5 iterations
Fits of model (![]() ) are plotted in Figure
) are plotted in Figure ![]() as solid
lines. Since the data set is small, different initial values
may lead to different estimates. However, the overall fits are similar.
We also fitted models with AR(1) within-subject correlations and covariate effects on
as solid
lines. Since the data set is small, different initial values
may lead to different estimates. However, the overall fits are similar.
We also fitted models with AR(1) within-subject correlations and covariate effects on
![]() . None of these models improve fits significantly. The estimates
are comparable to the nonlinear fits and the conclusion is similar to that
based on (
. None of these models improve fits significantly. The estimates
are comparable to the nonlinear fits and the conclusion is similar to that
based on (![]() ).
).
To check if the parametric NLMM (![]() ) is appropriate, we
calculated approximate posterior means and variances using the
function intervals. Then we plotted the estimated
) is appropriate, we
calculated approximate posterior means and variances using the
function intervals. Then we plotted the estimated ![]() (overall), its
projection onto
(overall), its
projection onto ![]() (the parametric part) and
(the parametric part) and ![]() (the smooth part) in Figure
(the smooth part) in Figure ![]() .
.
> co2.grid2 <- data.frame(u=seq(0.3, 11, len=50))
> co2.ci <- intervals(co2.fit2, newdata=co2.grid2,
terms=matrix(c(1,1,1,0,0,1), ncol=2,byrow=T))
> plot.bCI(co2.ci,x=co2.grid2$u,layout=c(3,1),
type.name=c("overall","parametric","smooth"))
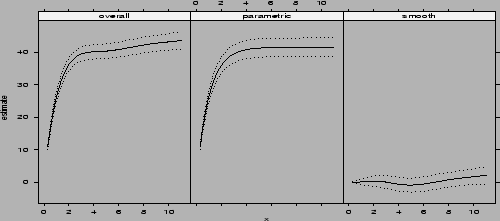 |
For ![]() -splines, Heckman and Ramsay (2000) showed that
selecting the right form of penalty function via a differential
operator
-splines, Heckman and Ramsay (2000) showed that
selecting the right form of penalty function via a differential
operator ![]() can reduce the bias. An
can reduce the bias. An ![]() -spline allows us to
incorporate prior knowledge on the main features of
-spline allows us to
incorporate prior knowledge on the main features of ![]() into the
penalty. Usually the form of
into the
penalty. Usually the form of ![]() is known with coefficients
depending on some unknown parameters. Heckman and Ramsay (2000)
proposed several methods to estimate these parameters. When the
whole model can be written in the form of an SNM model as in this
example, our methods can also be used to estimate the penalty.
Our approach is the same as the PL (penalized likelihood) approach
in Heckman and Ramsay (2000). They commented that the PL method is
``philosophically appealing''. However it is also ``time-consuming''
because a grid search was used. Our method estimates the coefficients
in
is known with coefficients
depending on some unknown parameters. Heckman and Ramsay (2000)
proposed several methods to estimate these parameters. When the
whole model can be written in the form of an SNM model as in this
example, our methods can also be used to estimate the penalty.
Our approach is the same as the PL (penalized likelihood) approach
in Heckman and Ramsay (2000). They commented that the PL method is
``philosophically appealing''. However it is also ``time-consuming''
because a grid search was used. Our method estimates the coefficients
in ![]() and the functions
and the functions ![]() iteratively, thus making it less
computationally intensive. In addition, we allow these coefficients
to depend on covariates.
iteratively, thus making it less
computationally intensive. In addition, we allow these coefficients
to depend on covariates.