


Next: The nnr Function
Up: Non-Parametric Nonlinear Regression Models
Previous: Non-Parametric Nonlinear Regression Models
In model (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) we have assumed that the function
) we have assumed that the function  is
observed through linear operators
is
observed through linear operators  's plus random errors.
Sometimes the function is observed indirectly which involves
nonlinear operators
(O'Sullivan, 1990; O'Sullivan and Wahba, 1985; Wahba, 1990; O'Sullivan, 1991; Wahba, 1987).
's plus random errors.
Sometimes the function is observed indirectly which involves
nonlinear operators
(O'Sullivan, 1990; O'Sullivan and Wahba, 1985; Wahba, 1990; O'Sullivan, 1991; Wahba, 1987).
We consider the following non-parametric nonlinear regression
(NNR) model
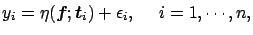 |
|
|
(30) |
where  is a known function of
is a known function of
 in an arbitrary domain
in an arbitrary domain  ,
,
 is a vector
of unknown non-parametric functions which act nonlinearly as
parameters of the function
is a vector
of unknown non-parametric functions which act nonlinearly as
parameters of the function  , and
, and
 are random errors distributed as
are random errors distributed as
 .
The functions
.
The functions  's could have the same or different domains.
We denote the model space of
's could have the same or different domains.
We denote the model space of  as
as
 |
|
|
(31) |
Let
 and
and
 .
We estimate
.
We estimate
 as the minimizer of the following penalized weighted
least squares
as the minimizer of the following penalized weighted
least squares
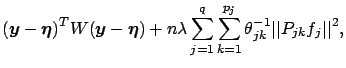 |
|
|
(32) |
where  is the orthogonal projection operator of
is the orthogonal projection operator of  onto
onto
 in
in  .
.
In the following we consider the special case when
 |
|
|
(33) |
where  is a known nonlinear function,
is a known nonlinear function,  's are
linear operators. (
's are
linear operators. (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) holds for most applications
and
) holds for most applications
and  's are usually the evaluational functionals. When
(
's are usually the evaluational functionals. When
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) does not hold, using linearization method, we
can approximate
) does not hold, using linearization method, we
can approximate
 by a linear combination
of linear operators.
by a linear combination
of linear operators.
When (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) holds, the solutions to (
) holds, the solutions to (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
have the form (
)
have the form (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ). Specifically,
). Specifically,
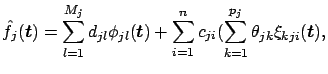 |
|
|
(34) |
where
 are bases of
are bases of  ,
,
 ,
and
,
and  is the rk of
is the rk of  . We estimate coefficients
. We estimate coefficients
 's and
's and  's using (
's using (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) with
) with  's being
replaced by (
's being
replaced by (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ). Since
). Since  in (
in (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) is
nonlinear, an iterative method has to be used to solve these
coefficients. Two methods are used: the Gauss-Newton and
Newton-Raphson procedures. See Ke and Wang (2002) for more details.
) is
nonlinear, an iterative method has to be used to solve these
coefficients. Two methods are used: the Gauss-Newton and
Newton-Raphson procedures. See Ke and Wang (2002) for more details.



Next: The nnr Function
Up: Non-Parametric Nonlinear Regression Models
Previous: Non-Parametric Nonlinear Regression Models
Yuedong Wang
2004-05-19
![]() ) we have assumed that the function
) we have assumed that the function ![]() is
observed through linear operators
is
observed through linear operators ![]() 's plus random errors.
Sometimes the function is observed indirectly which involves
nonlinear operators
(O'Sullivan, 1990; O'Sullivan and Wahba, 1985; Wahba, 1990; O'Sullivan, 1991; Wahba, 1987).
's plus random errors.
Sometimes the function is observed indirectly which involves
nonlinear operators
(O'Sullivan, 1990; O'Sullivan and Wahba, 1985; Wahba, 1990; O'Sullivan, 1991; Wahba, 1987).
![]() and
and
![]() .
We estimate
.
We estimate
![]() as the minimizer of the following penalized weighted
least squares
as the minimizer of the following penalized weighted
least squares
![]() ) holds, the solutions to (
) holds, the solutions to (![]() )
have the form (
)
have the form (![]() ). Specifically,
). Specifically,